사이킷런은 ML 모델 학습을 위해서 fit( )을,
학습된 모델의 예측을 위해 predict( ) 메소드를 제공한다.
사이킷런에서는 분류 알고리즘을 구현한 클래스를 Classifier로,
그리고 회귀 알고리즘을 구현한 클래스를 Regressor로 지칭한다.
이 두가지를 합쳐서 Estimator 클래스라고 부른다.
즉, 지도학습의 모든 알고리즘을 구현한 클래스를 통칭해서 Estimator라고 부른다.
cross_val_score( )와 같은 evaluation 함수, GridSearchCV와 같은 하이퍼 파라미터 튜닝을
지원하는 클래스의 경우 이 Estimator를 인자로 받는다.
인자로 받은 Estimator에 대해서 cross_val_score( ), GridSearchCV.fit( ) 함수 내에서
이 Estimator의 fit( )과 predict( )를 호출해서 평가를 하거나 하이퍼 파라미터 튜닝을
수행하는 것이다.

사이킷런에서 비지도학습인 차원 축소, 클러스터링, 피처 추출(Feature Extraction) 등을
구현한 클래스 역시 대부분 fit( )과 transform( )을 적용한다.
비지도학습과 피처 추출에서 fit( )은 지도학습의 fit( )과 같이 학습을 의미하는 것이
아니라 입력 데이터의 형태에 맞춰 데이터를 변환하기 위한 사전 구조를 맞추는 작업이다.
fit( )으로 변환을 위한 사전 구조를 맞추면 이후 입력 데이터의 차원 변환, 클러스터링, 피처 추출 등의
실제 작업은 transform( )으로 수행한다. 사이킷런은 fit( )과 transform( )을 하나로 결합한
fit_transform( )도 제공하지만 사용 시에 주의가 필요하다.
♧ 사이킷런의 주요 모듈
|
분류 |
모듈명 |
설명 |
|
예제 데이터 |
sklearn.datasets |
사이킷런에 내장되어 예제로 제공하는 데이터 세트 |
|
피처처리 |
sklearn.preprocessing |
데이터 전처리에 필요한 다양한 가공 기능 제공(문자열을 숫자형 코드 값으로 인코딩, 정규화, 스케일링 등) |
|
sklearn.feature_selection |
알고리즘에 큰 영향을 미치는 피처를 우선순위대로 셀렉션 작업을 수행하는 다양한 기능 제공 |
|
|
sklearn.feature_extraction |
텍스트 데이터나 이미지 데이터의 벡터화된 피처를 추출하는데 사용됨. 예를 들어 텍스트 데이터에서 Count Vectorizer나 Tf-Idf Vectorizer 등을 생성하는 기능 제공. 텍스트 데이터의 피처 추출은 sklearn.feature_extraction.text 모듈에, 이미지 데이터의 피처 추출은 sklearn.feature_extraction.image 모듈에 지원 API가 있음 |
|
|
피처 처리 & 차원 축소 |
sklearn.decomposition |
차원 축소와 관련한 알고리즘을 지원하는 모듈이다. PCA, NMF, Truncated SVD 등을 통해 차원 축소 기능을 수행할 수 있다. |
|
데이터 분리, 검증 & 파라미터 튜닝 |
sklearn.model_selection |
교차 검증을 위한 학습용/테스트용 분리, 그리드 서치(Grid Search)로 최적 파라미터 추출 등의 API 제공 |
|
평가 |
sklearn.metrics |
분류, 회귀, 클러스터링, 페어와이즈(Pairwise)에 대한 다양한 성능 측정 방법 제공 Accuracy, Precision, Recall, ROC-AUC, RMSE 등 제공 |
|
ML 알고리즘 |
sklearn.ensemble |
앙상블 알고리즘 제공 랜덤 포레스트, 에이다 부스트, 그래디언트 부스팅 등을 제공 |
|
sklearn.linear_model |
주로 선형 회귀, 릿지(Ridge), 라쏘(Lasso) 및 로지스틱 회귀 등 회귀 관련 알고리즘을 지원. 또한 SGD(Stochastic Gradient Desccent) 관련 알고리즘도 제공 |
|
|
sklearn.naïve_bayes |
나이브 베이즈 알고리즘 제공. 가우시안 NB. 다항 분포 NB 등 |
|
|
sklearn.neighbors |
최근접 이웃 알고리즘 제공. K-NN(K-Nearest Neighborhood) 등 |
|
|
sklearn.svm |
서포트 벡터 머신 알고리즘 제공 |
|
|
sklearn.tree |
의사 결정 트리 알고리즘 제공 |
|
|
sklearn.cluster |
비지도 클러스터링 알고리즘 제공 (K-평균, 계층형, DBSCAN 등) |
|
|
유틸리티 |
sklearn.pipeline |
피처 처리 등의 변환과 ML 알고리즘 학습, 예측 등을 함께 묶어서 실행할 수 있는 유틸리티 제공 |
♧ KNN(K - Nearest Neighborhood)




이 예시는 초록색 별이 어떤 영화인지(액션 vs 로맨스)를 구분하기 위한 예시다.
각각의 축은 영화에서 나오는 장면의 횟수인데 y축은 발차기 횟수, x축은 키스 횟수이다.
동그랗게 원을 그려보면 원 안에 발차기 횟수가 더 많은 것을 알 수 있다.
따라서 이 영화는 액션 영화에 더 가깝게 분류된다고 볼 수 있다.
만약 k를 짝수로 정해준다면 세번째 그림(왼쪽 아래)과 같이 구분할 수가 없게된다.
따라서 k는 보통 홀수로 지정하게 된다. 최근접점을 구하기 위해 피타고라스 정리를 사용하여 거리를 구한다.
♧ Decision Tree
데이터를 가지고 있을 때 이 데이터를 분류하기 가장 좋은 질문을 함으로써 클래스를 분류하는 지도학습이다.


애기한테 겨울 가족(인간) 사진을 골라보라고 한다면 어떻게 분류할까? 정답은 1장 밖에 없다.
의사결정나무 알고리즘에 따라서 캐릭터인지 아닌지, 겨울인지 아닌지, 사람이 1명인지 아닌지를 판단한다.

문제는 미리 문제를 규정해줘야 한다는 것과 학습 자료를 수집해야 된다는 것이다.
얘가 고양이야라고 알려주고 학습시켜야 분류할 수 있다는 것이다. (Supervised Learning)


의사결정나무를 만들고, 각 노드에 따라서 분류되는 사진들의 결과는 다음과 같다. (ID3 알고리즘)

이렇게 정리된 사진들로 엔트로피[높은 엔트로피: 어질러진 방/ 낮은 엔트로피: 잘 정리된 방]를 계산하면 사진과 같다.
총 8장의 사진 중에 1장만이 겨울가족사진이므로 엔트로피는
(1장만 해당되고, 나머지 7장은 아니다) = 0.543으로 계산된다.
Information Gain = 주어진 상황 - 하나의 속성을 잡았을 때의 엔트로피

첫번째 식은 계산했던 0.543에서 만화를 속성으로 잡은 엔트로피를 빼는 식이다.
0.543 - (만화에 해당하는 사진 수 4개/총사진수 8개 * E([겨울가족사진해당수 0개, 겨울가족여행사진아닌거 4개)] + 만화가 아닌 사진 4개/총 사진 8개 * E([만화가 아닌 사진 4개 중 오직 1개의 사진만 겨울가족사진, 나머지 3개는 아닌거])
= 0.138이 나온다.
이런 식으로 두번재는 겨울을 속성으로 잡았고, 세번째는 한사람 이상인 것을 기준으로 잡았다.
이 중 인포메이션 게인이 가장 높은 값을 속성으로 잡아주면 된다.
♧ Random Forest
의사결정나무는 하나의 거대한 나무로 보면 되고, 랜덤포레스트는 작은 나무(생김새 다름)로 구성된 하나의 숲이다.


사과와 오렌지 분류하기
첫번째 특징은 부스팅이다. 의사결정나무는 8개의 데이터가 있으면 모두 사용한다.
랜덤포레스트는 나무당 3개(임의)씩 데이터를 주었다. 자세히 보면 같은 그림이 있음을 확인할 수 있다.
랜덤포레스트의 경우 중복이나 반복된 데이터를 허용함으로써 모델의 편향이 올라가게 된다.
의사결정나무의 경우 오버피팅이 되기 쉽다.

이 때 부스팅 때문에 편향이 올라가는 랜덤포레스트가 의사결정나무의 오버피팅에 솔루션으로 사용될 수도 있다.
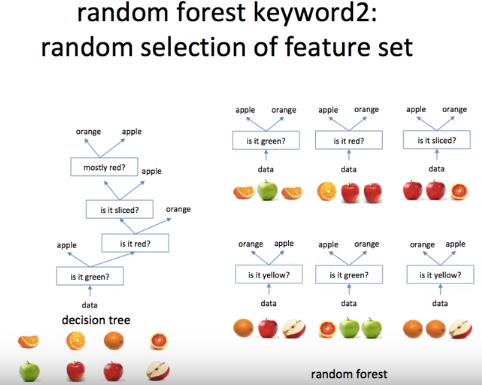
의사결정나무는 항상 가장 좋은 질문을 먼저 하게 되어있다.
랜덤포레스트는 질문이 랜덤으로 가장 좋은 질문이 아닐 수 있다.
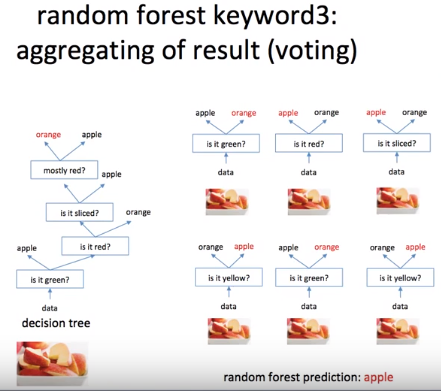
오른쪽 사진의 경우 잘려진 사과를 테스트 데이터로 주었을 때, 의사결정나무는 orange로 분류했고
랜덤포레스트는 사과로 분류했다. 랜덤포레스트의 경우 aggregating(투표)를 통해 사과로 예측하였는데
이 또한 특징이라고 할 수 있다. (사과가 4표고 오렌지가 2표)
즉, 더 많은 결과값이 있는 것을 따른다.
♧ 나이브 베이즈(Naive Bayes)

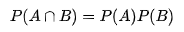
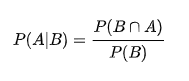
나이브 베이즈 분류는 텍스트 분류에 사용됨으로써 문서를 여러 범주 (예: 스팸, 스포츠, 정치)중 하나로 판단하는 문제에 대한 대중적인 방법으로 남아있다. 또한, 자동 의료 진단 분야에서의 응용사례를 보면, 적절한 전처리를 하면 더 진보 된 방법들 (예: 서포트 벡터 머신 (Support Vector Machine))과도 충분한 경쟁력을 보임을 알 수 있다.
모든 나이브 베이즈 분류기는 공통적으로 모든 특성 값은 서로 독립임을 가정한다.
예를 들어, 특정 과일을 사과로 분류 가능하게 하는 특성들(둥글다, 빨갛다, 지름 10cm)은 나이브 베이즈 분류기에서
특성들 사이에서 발생할 수 있는 연관성이 없음을 가정하고 각각의 특성들이 특정 과일이 사과일 확률에
독립적으로 기여하는 것으로 간주한다.
나이브 베이즈의 장점
- 일부의 확률 모델에서 나이브 베이즈 분류는 지도 학습(Supervised Learning) 환경에서 매우 효율적으로 훈련 될 수 있다.많은 실제 응용에서 나이브 베이즈 모델의 파라미터 추정은 최대우도방법(Maximum Likelihood Estimation (MLE))을 사용하며, 베이즈 확률론이나 베이지안 방법들은 이용하지 않고도 훈련이 가능하다.
- 분류에 필요한 파라미터를 추정하기 위한 트레이닝 데이터의 양이 매우 적다는 것다는 것이다.
- 간단한 디자인과 단순한 가정에도 불구하고, 나이브 베이즈 분류는 많은 복잡한 실제 상황에서 잘 작동한다.
베이즈 추정법의 기본 원리
수학적으로 베이즈 추정법은 주어진 데이터 {x1,…,xN}{x1,…,xN}를 기반으로 모수 μ의 조건부 확률분포 p(μ|x1,…,xN)p(μ|x1,…,xN)를 계산하는 작업이다. 조건부 확률분포를 구하므로 베이즈 정리를 사용한다.


p(μ)는 모수의 사전(Prior)분포다. 사전 분포는 베이지안 추정 작업을 하기 전에 이미 알고 있던 모수 μ의 분포를 뜻한다.
모수에 대해 모르는 경우에는 균일(uniform) 분포 Beta(1,1)나 0을 중심으로 가지는 정규분포 N(0, 1) 등의
무정보분포(non-informative distribution)를 사용할 수 있다.
-
p(μ∣x1,…,xN)는 모수의 사후(Posterior)분포다. 수학적으로는 데이터 x1,…,xN가 주어진 상태에서의 μ에 대한 조건부 확률 분포다. 우리가 베이즈 추정법 작업을 통해 구하고자 하는 것이 바로 이 사후 분포다.
- p(x1,…,xN∣μ)는 가능도(likelihood)분포다. 모수 μ가 특정한 값으로 주어졌을 때 주어진 데이터{x1,…,xN}가 나올 수 있는 확률값을 나타낸다.

즉, 다시 정리하면 사후확률은 위와 같다.
(where posterior = 사후확률, prior = 사전확률, likelihood = 가능도, evidence = 관찰값 )
이때 계산된 모수의 분포는 두 가지 방법으로 표현한다.
(1) 모수적(parametric) 방법
- 다른 확률분포를 사용하여 추정된 모수의 분포를 나타낸다. 모수 분포를 표현하는 확률분포함수의 모수를 하이퍼모수(hyper-parameter)라고 부른다. 모수적 방법을 사용한 베이즈 추정법은 결국 하이퍼모숫값을 계산하는 작업이다.
(2) 비모수적(non-parametric) 방법
- 모수의 분포와 동일한 분포를 가지는 실제 표본 집합을 생성하여 히스토그램이나 최빈값 등으로 분포를 표현한다. MCMC(Markov chain Monte Carlo)와 같은 몬테카를로(Monte Carlo) 방법이 비모수적 방법이다.
😁
출처:

https://www.youtube.com/channel/UCxP77kNgVfiiG6CXZ5WMuAQ
Minsuk Heo 허민석
Tutorial for Computer Science
www.youtube.com
https://datascienceschool.net/view-notebook/ae35a40deb884cf88e85135b4b5a1130/
Data Science School
Data Science School is an open space!
datascienceschool.net
https://ko.wikipedia.org/wiki/%EC%A1%B0%EA%B1%B4%EB%B6%80_%ED%99%95%EB%A5%A0
조건부 확률 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 둘러보기로 가기 검색하러 가기 조건부 확률(conditional probability)은 어떤 사건 B가 일어났을 때 사건 A가 일어날 확률을 의미한다. 사건 B가 발생했을 때 사건 A가 발생하는 도수(혹은 수량)는 사건 B의 영향을 받아 변하는데 이를 조건부 확률이라 한다. 기호로는 P ( A | B ) {\displaystyle P(A|B)} 으로 표현한다. 확률 공간 Ω에서의 두 사건 A, B에 대해서 P ( B )
ko.wikipedia.org
나이브 베이즈 분류 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 둘러보기로 가기 검색하러 가기 기계 학습분야에서, '나이브 베이즈 분류(Naïve Bayes Classification)는 특성들 사이의 독립을 가정하는 베이즈 정리를 적용한 확률 분류기의 일종으로 1950 년대 이후 광범위하게 연구되고 있다. 통계 및 컴퓨터 과학 문헌에서 , 나이브 베이즈는 단순 베이즈, 독립 베이즈를 포함한 다양한 이름으로 알려져 있으며, 1960 년대 초에 텍스트 검색 커뮤니티에 다른 이름으로 소개
ko.wikipedia.org
'Data Scientist' 카테고리의 다른 글
| 웹크롤링(Selenium) 간단한 검색, 네이버 로그인, yes24검색 후 장바구니 담기 (0) | 2020.02.26 |
|---|---|
| 웹크롤링(Requests & BeautifulSoup) (0) | 2020.02.26 |
| sklearn 기초 - 붓꽃 품종 예측하기 (0) | 2020.02.23 |
| 군집화(K-means clustering) (0) | 2020.02.16 |
| 빅데이터를 지배하는 통계의 힘 (0) | 2020.02.11 |



