♣ 통계적 가설검정의 이해
1-1. 통계적 가설 검정의 단계
- 가설검정
- 유의수준을 통해 의사결정 규칙 정하기
- 검정통계량 계산
- 통계적 의사결정과 해석
1-2. 통계적 가설 설정
대립가설, 연구가설(Ha 또는 H₁)
- 연구자가 증명하고 싶었던 가설
- ex) xx의 효과가 있다. 차이가 있다
영가설, 귀무가설(H0)
- 연구자가 증명하기를 원했던 가설의 반대가설
- ex) xx의 효과가 없다. 차이가 없다
- 연구자는 먼저 영가설이 옳다고 가정하고 검정을 진행함 -> 연구자는 귀무가설을 기각하고 대립가설을 채택하기를 원한다.
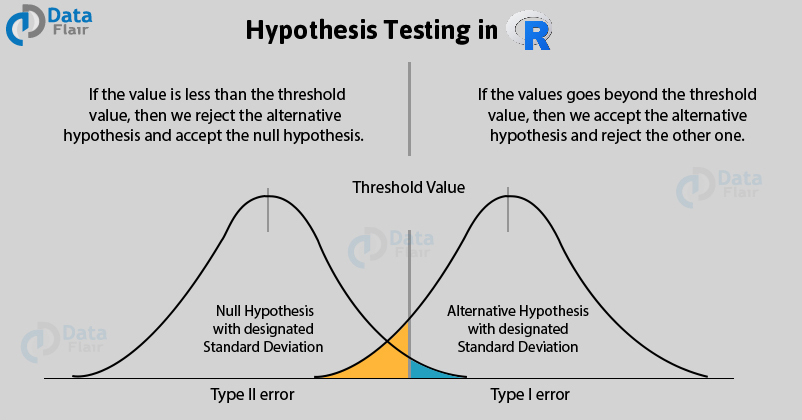


통계적 가설 검정은
1. 표본에서 검정통계량(test statistic)을 계산함으로써 시작
- 검정통계량이란 자료를 하나 또는 적은 수의 숫자로 요약되는 것




2. 그 검정통계량이 따르는 분포(표집분포, sampling distribution)를 결정
3. 검정통계량이 영가설이 옳다는 가정하의 표집분포 상에서 일반적으로 발생할 수 있는지 아니면 매우 드문 일인지를 판별
- 일반적인 값이라면 H0(귀무가설)을 기각하는데 실페
- 매우 드문 값이라면 H0를 기각
즉, 통계적 가설 검정은 영가설(ex. 두 표본이 같은 모집단에서 나왔다, 두 표본의 평균이 같다)이 기각될 수 있는가를 통계적으로(확률적으로) 결정하는 작업
통계적 가설의 형태로 영가설과 대립가설을 표기할 때, 이는 모집단의 분포나 모수치에 대한 잠정적 진술이므로 모수치에 대하여 표기해야 한다. 가설검정은 모집단의 속성을 추리하기 때문이다.
검정을 실시할 때, 우리는 다음의 두 가지 결론에 도달한다.
1) 영가설을 기각한다(reject H0)
2) 영가설을 기각하는데 실패한다(fail to reject H0)
검정은 확률에 기반한 것이기 때문에, 어떤 결정을 내리든 간에 그것은 옳은 결정일 수도 잘못된 결정일 수도 있다.
1-3. 의사결정의 오류
통계적 가설 검정시에는 다음의 두 가지 실수를 범할 수가 있다.
| 진실 | |||
| H0이 사실(효과 없음) | H0이 거짓(효과 있음) | ||
| 통계적 의사결정 | H0 기각(H1 선택, 효과 있음) | 1종 오류(α) |
Correct 검정력(power) (1 - β) |
| H0 기각 실패(효과 없음) | Correct | 2종 오류(β) | |
* 1종오류와 유의수준은 수학적으로 같은 개념이며, 관점에 따라 다른 이름으로 불리는 것
♧ 유의수준(significance level, α)
- 영가설이 옳다는 가정하에서 검정통계량이 얼마나 극단적이어야 그것을 극단적이라고 결론 내리고 영가설을 기각하게 될 것인가의 정도
- 유의수준을 통해 의사결정 규칙 설정
- α는 자료의 수집이나 분석 이전에 미리 결정하며, 사회과학에서는 5% 양방검정을 많이 사용
우리는 모집단을 통째로 조사하지 않는 한 진실을 알 수 없으므로 영가설을 기각하는 통계적 결정을 했을 때 1종 오류를 범했을 수도 있고 그렇지 않을 수도 있다.
통계적 결정을 하는 데 있어서 유의수준이란 것은 우리가 범할 수 있는 1종 오류 확률의 한계를 지어놓은 것으로 이해할 수 있다. 즉, 유의수준 5%에서 검정을 하는 것은 검정과정에서 1종 오류를 범할 수도 있고 범하지 않을 수도 있는데 만약 범했을 경우에 최대 5% 이내의 확률로 범하게 되는 것이다.
♧ 제 1종 오류(Type I error, α)
- 귀무가설이 사실인데도 불구하고 귀무가설을 기각할 확률
- 일반적으로 제 1종오류를 범하는 것은 제 2종오류를 범하는 것보다 더욱 심각한 문제로 인식된다. 그 이유는 존재하지 않는 효과(effect)를 기각함으로써 보여주었기 때문이다.
♧ 제 2종오류(Type II error, β)
- 귀무가설이 사실이 아닐 때, 귀무가설을 기각하는데 실패하게 될 확률
♧ 검정력(power)
- 귀무가설이 사실이 아닐 때, 귀무가설을 기각할 확률( 1 - β)
- 당연히 옳은 결정이며, 통계 검정에서 매우 중요하게 취급됨
- 연구자가 계획한 처치가 정말 효과가 있을 떄 그것이 효과가 있다고 결론 내릴 수 있는 확률
* 검정력에 영향을 줄 수 있는 요인
- 효과크기(effect size)
- 연구자가 시행한 처치효과의 크기, 연구자가 통제하기 어려움
- 효과크기 ▲ → 검정력 ▲
- 유의수준(5%)
- 검정의 방향성(양방검정)
- 표본크기
- 표본크기▲ → 표집분포의 표준오차▼ → 검정력▲
- 검정력 증가시키기 위해 연구자가 선택할 수 있는 가장 적절한 방법
1-4. 검정통계량 계산
검정 방법에 따라 t, z, x², F 등의 검정통계량 사용
1-5. 통계적 의사결정과 해석
♧ p-value
- 귀무가설이 옳다는 가정하에 검정통계량이 이론적으로 따르는 표집분포상에서 표본에 기반한 검정통계량보다 더 극단적일 확률
- 유의확률 X
1-6. 그 외의 주요 개념
♧ 효과크기
통계적으로 유의한 결과를 얻었다는 것이 실용적으로도 유의한 결과를 얻었다는 것을 의미할까?
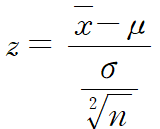
- 분자인 평균차이가 같아도
- 표본크기 n▲ →분모의 표준오차 ▼ → z검정통계량▲ → 영가설 기각
매우 작은 평균의 차이조차도 큰 표본하에서는 통계적으로 유의한 검정 결과를 줄 수 있다.(통계적 가설검정의 약점)
Cohen(1988) 효과크기를 이용하여 실용적인 효과의 크기를 측정할 것을 제안
어떤 통계모형을 사용하는지 및 어떤 검정방법을 사용하는지 등에 따라 매우 다양한 형태로 존재
- 단일표본 z 검정에서 효과크기의 모수 σ

- 단일표본 z 검정에서 효과크기 추정치(Cohen's d)

♧ 신뢰구간
* 점추정(point estimation): 하나의 값으로 모수를 추정하는 것
점추정치는 매우 정밀하지만(precise), 정확성에 대해서는 그다지 확신할 수 없다(less confident).
* 구간추정(interval estimation): 모수가 속할 범위를 추정하는 것
구간추정치는 점추정치에 비해 정밀성은 떨어지지만(less precise) 더 많은 정보를 주어 더 높은 확신(more confident)을 제공
- 모수의 구간추정치가 실제로 모수를 포함하고 있을거라는 확신
- 확신의 수준(confidence level): 구간이 넓을수록 강해짐(정밀도는 낮아짐)
우리가 원하는 것은 되도록 정밀한 구간추정치로 높은 수준의 확신을 달성하는 것
- 95% 신뢰구간

신뢰구간의 너비(확신의 수준)에 표준오차가 직접 영향을 미침
- 표본크기▲ → 표집분포의 표준오차 ▼ → 신뢰구간좁아짐, 신뢰구간의유용성▲
😁
출처:
심미경님
김수영(2019). 사회과학통계의 기본. 서울: 학지사.
성태제(2015). 현대 기초통계학. 서울: 학지사.
오만숙(2017). 베이지안 통계추론. 서울: 자유아카데미.
https://data-flair.training/blogs/hypothesis-testing-in-r/
Introduction to Hypothesis Testing in R - Learn every concept from Scratch! - DataFlair
With this R hypothesis testing tutorial, learn about the decision errors, two-sample T-test with unequal variance, one-sample T-testing, formula syntax and subsetting samples in T-test and μ test in R.
data-flair.training
http://blog.naver.com/PostView.nhn?blogId=jake1125&logNo=220656645340
가설검정 - 유의, 귀무가설, 오류, 검정력
통계와 데이터를 다룰 때, 모집단 보다 표본을 다루는 경우가 대다수이다. 만약 표본 데이터에 불규칙성이 ...
blog.naver.com
https://slideplayer.com/slide/3027537/
Hypothesis Testing. To define a statistical Test we 1.Choose a statistic (called the test statistic) 2.Divide the range of possi
To perform a statistical Test we 1.Collect the data. 2.Compute the value of the test statistic. 3.Make the Decision: If the value of the test statistic is in the Acceptance Region we decide to accept H 0. If the value of the test statistic is in the Critic
slideplayer.com
'Data Scientist' 카테고리의 다른 글
| 통계기초(베이지안 통계) (0) | 2020.03.09 |
|---|---|
| 통계기초(상관관계 ,공분산) (0) | 2020.03.08 |
| 통계기초(표집이론) (0) | 2020.03.04 |
| 통계기초(자료의 중심과 퍼짐) (0) | 2020.03.03 |
| 통계기초(모집단, 변수, 측정,무선표집과 무선할당) (0) | 2020.03.02 |



